Introduction
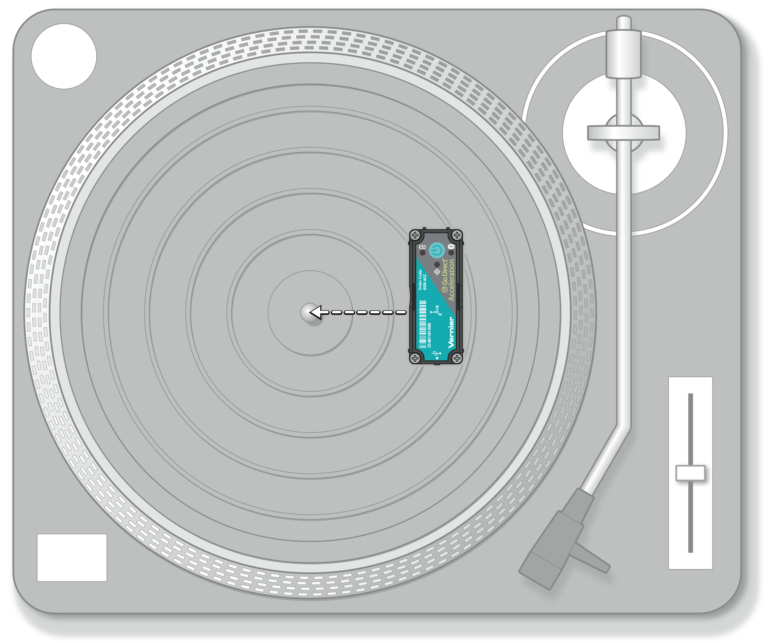
As a child, you may remember the challenge of spinning a playground merry-go-round so you could scare the unfortunate riders as they traveled around a circular path. You worked especially hard to push the merry-go-round to increase its angular velocity. As the angular velocity of the riders increased, so did their centripetal acceleration. The challenge for the riders was to compete with the centripetal acceleration to maintain their grip—and their stomachs. The faster the merry-go-round was spun, the more difficult it became to stay on the ride. It may have disappointed you when the riders cheated and moved toward the center of the merry-go-round to reduce the acceleration. In this activity, you will investigate centripetal acceleration on a turntable. You will use a Low-g Accelerometer or Wireless Dynamics Sensor System (WDSS) attached to the turntable to determine the relationship between centripetal acceleration, angular velocity, and the radius of the circular path.
Objectives
- Measure centripetal acceleration on a record turntable.
- Determine the relationship between centripetal acceleration, radius, and angular velocity.
- Determine the direction of centripetal acceleration.
Sensors and Equipment
This experiment features the following sensors and equipment. Additional equipment may be required.
Correlations
Teaching to an educational standard? This experiment supports the standards below.
- International Baccalaureate (IB) 2025/Physics
- The students should understand that bodies moving along a circular trajectory at a constant speed experience an acceleration that is directed radially towards the centre of the circle—known as a centripetal acceleration as given by a = v2/r = w2r=4π2r/T2
- The students should understand that circular motion is caused by a centripetal force acting perpendicular to the velocity
- The students should understand that a centripetal force causes the body to change direction even if its magnitude of velocity may remain constant
- The students should understand that the motion along a circular trajectory can be described in terms of the angular velocity ω which is related to the linear speed v by the equation as given by v=2πr/T=wr
Ready to Experiment?
Ask an Expert
Get answers to your questions about how to teach this experiment with our support team.
- Call toll-free: 888-837-6437
- Chat with Us
- Email support@vernier.com
Purchase the Lab Book
This experiment is #20 of Physics with Vernier. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.







