Introduction
Lots of things vibrate or oscillate. A vibrating tuning fork, a moving child’s playground swing, and the loudspeaker in a radio are all examples of physical vibrations. There are also electrical and acoustical vibrations, such as radio signals and the sound you get when blowing across the top of an open bottle.
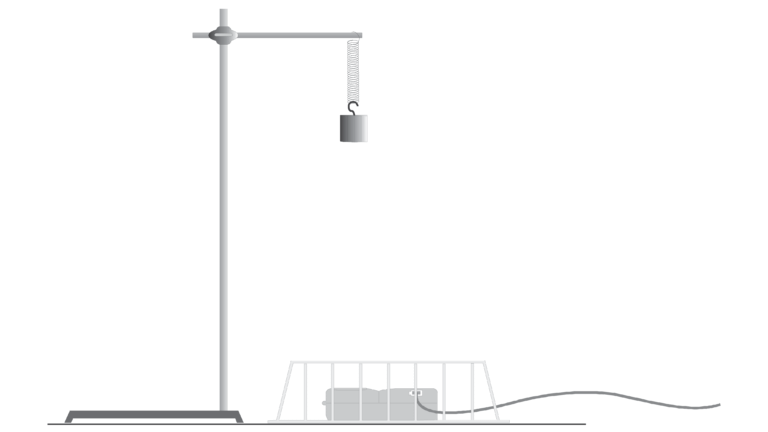
One simple system that vibrates is a mass hanging from a spring. The force applied by an ideal spring is proportional to how much it is stretched or compressed. Given this force behavior, the up and down motion of the mass is called simple harmonic and the position can be modeled with
In this equation, y is the vertical displacement from the equilibrium position, A is the amplitude of the motion, f is the frequency of the oscillation, t is the time, and φ is a phase constant. This experiment will clarify each of these terms.
Objectives
- Measure the position and velocity as a function of time for an oscillating mass and spring system.
- Determine the amplitude, period, and phase constant of the observed simple harmonic motion.
- Compare the observed motion of a mass and spring system to a mathematical model of simple harmonic motion.
Sensors and Equipment
This experiment features the following sensors and equipment. Additional equipment may be required.
Correlations
Teaching to an educational standard? This experiment supports the standards below.
- International Baccalaureate (IB) 2025/Physics
- The students should understand a particle undergoing simple harmonic motion can be described using time period T, frequency ƒ, angular frequency ω, amplitude, equilibrium position, and displacement
- The students should understand the time period in terms of frequency of oscillation and angular frequency as given by T = 1/ƒ = 2π/ω
- The students should understand the time period of a mass–spring system as given by T = 2π √m/k
Ready to Experiment?
Ask an Expert
Get answers to your questions about how to teach this experiment with our support team.
- Call toll-free: 888-837-6437
- Chat with Us
- Email support@vernier.com
Purchase the Lab Book
This experiment is #15 of Physics with Vernier. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.






