The Mathematical Model of Simple Harmonic Motion
Experiment #15 from Advanced Physics with Vernier — Mechanics
- Subject
- Physics
Introduction
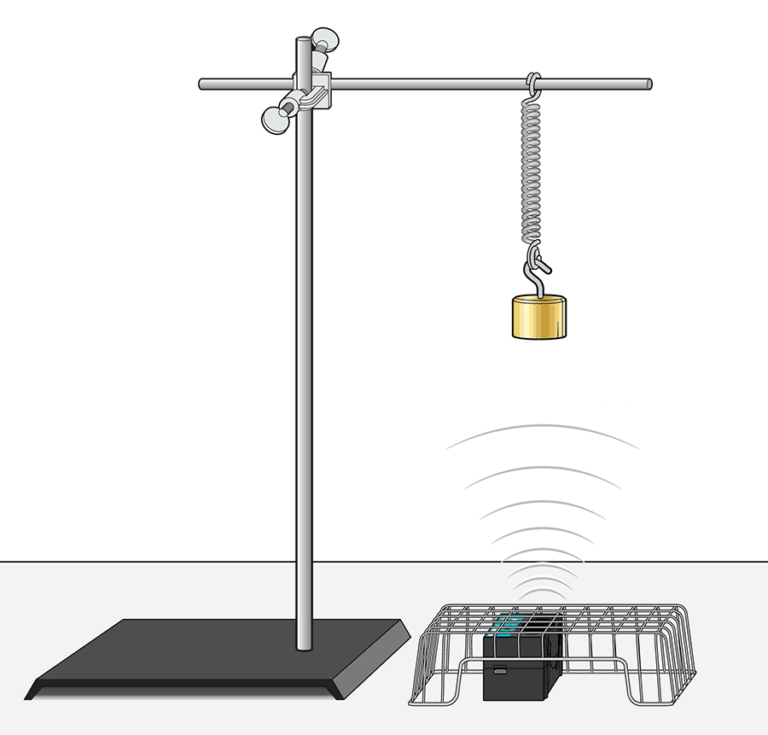
When you suspend an object from a spring, the spring will stretch. If you pull on the object and release it, it will begin to oscillate up and down. In this experiment, you will examine this kind of motion, perform a curve fit on the position-time graph, and relate the parameters of the equation with physical features of the system.
Objectives
In this experiment, you will
- Collect position vs. time data as a mass, hanging from a spring, is set in an oscillating motion.
- Determine the best fit equation for the position vs. time graph of an object undergoing simple harmonic motion (SHM).
- Define the terms amplitude, offset, phase shift, period and angular frequency in the context of SHM.
- Relate the parameters in the best-fit equation for a position vs. time graph to their physical counterparts in the system.
- Use deductive reasoning to predict the system mass required to produce a given value of angular frequency in the curve fit to SHM.
Sensors and Equipment
This experiment features the following sensors and equipment. Additional equipment may be required.
Option 1

Option 2

Correlations
Teaching to an educational standard? This experiment supports the standards below.
- International Baccalaureate (IB) 2025/Physics
- The students should understand a particle undergoing simple harmonic motion can be described using time period T, frequency ƒ, angular frequency ω, amplitude, equilibrium position, and displacement
- The students should understand the time period in terms of frequency of oscillation and angular frequency as given by T = 1/ƒ = 2π/ω
- The students should understand the time period of a mass–spring system as given by T = 2π √m/k
Ready to Experiment?
Ask an Expert
Get answers to your questions about how to teach this experiment with our support team.
- Call toll-free: 888-837-6437
- Chat with Us
- Email support@vernier.com
Purchase the Lab Book
This experiment is #15 of Advanced Physics with Vernier — Mechanics. The experiment in the book includes student instructions as well as instructor information for set up, helpful hints, and sample graphs and data.

